


|
приложение сайта
ФИЗИКА ВОКРУГ НАС и в лицее 1501 |
|
beta версия |
|
Статья «Фотографирование невозможных объектов» микропроект Орехова Вадима 2005-2006 учебный год |
|
Обычные двумерные фотографии и рисунки можно рассматривать двояко. С одной стороны – это система линий на плоскости, с другой – изображение объектов совсем иного, трёхмерного пространства. В мозгу информация перерабатывается, и мы воссоздаём по имеющемуся двумерному изображению трёхмерный мир. Подобный процесс происходит не только при рассматривании двумерных фотографий и рисунков. Известно, например, что на сетчатке глаза всё отражается в перевёрнутом виде, но мы воспринимаем изображение как нормальное. Можно надеть особые очки и попытаться видеть мир перевёрнутым. Однако вскоре мозг приспосабливается, и изображение вновь будет восприниматься как нормальное. Таким образом, мозг постоянно перерабатывает получаемую зрительную информацию и согласовывает её с информацией, получаемой от остальных органов чувств. Так вырабатывается наше представление об окружающем мире. |
|
Иногда из двумерного рисунка или фотографии мозг не может однозначным образом построить реально существующий трёхмерный объект. Такие объекты получили название невозможных. Хотя реально эти объекты не существуют, можно всё-таки сделать трёхмерную модель, которая создаёт впечатление невозможно объекта, если её сфотографировать из определённой точки. Например, изображённый на рисунке 1 невозможный треугольник, придуманный Пенроузом, можно получить, сделав разомкнутую трёхмерную модель (рис. 2). Если смотреть на такую модель одним глазом и найти нужную точку, можно увидеть, как две разъединённые стороны модели совместятся. Сфотографировав модель из этого положения, получится фотография невозможного треугольника Пенроуза. |
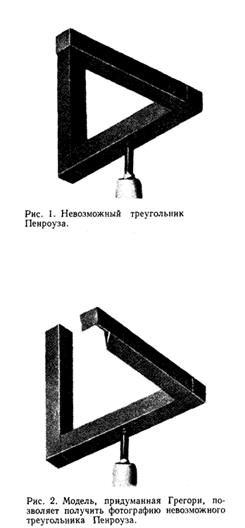



|
Из плотного цветного картона сделаем клетку, которая изображена на рисунке 4. В левой и нижней передних ребрах сделаем прорези (смотри рисунок 5). Расположив её так, чтобы задние ребра клетки закрыли прорези в передних, мы увидим невозможный куб: задние ребра клетки будут казаться выдвинутыми вперёд. Из этого положения можно получить и фотографию невозможного куба (рис.3). |
|
Рис. 3. Фотография невозможного куба. |
|
Рис. 4. |
|
Рис. 5. |
|
Физиолог Гибсон, использовав эту идею, придумал ряд интересных иллюзий, в которых он использовал картонные прямоугольники с прорезями в некоторых из них, для того чтобы более удалённый из прямоугольников казался расположенным на переднем плане. На рисунке 4 два набора квадратов, хотя и кажутся одинаковыми, по-разному расположены в пространстве, а в третьем ряду валет находится ближе шестёрки, и карты, следовательно, одинаковы по размеру. Такую фотографию можно получить, сделав соответствующие прорези в ближе расположенной карте и в среднем прямоугольнике, через которые можно увидеть более удалённую шестёрку (рис. 6). |

|
Рис. 6. |
|
Получим фотографию, аналогичную иллюзиям Гибсона (рис. 7).Сделаем фотографию вида из окна через оконное стекло. Сделаем увеличенную копию обложки задачника и приложим её к оконному стеклу так, чтобы копия обложки задачника закрывала от объектива фотоаппарата часть дома. Заметим на обложке точки пересечения её контуров с контурами дома. Доведём фотографию с изображением дома до таких размеров, чтобы, очертания дома соответствовали отмеченным на обложке точкам. Сделаем из этой фотографии шаблон изображения дома. Наложим шаблон на обложку и обведём его по точкам, отмеченным на ней. Вырежем обведённую часть обложки (рис. 8). Зафиксируем копию обложки задачника на оконном стекле на прежнем месте. Скорректируем положение объектива фотоаппарата до полного совпадения изображения дома с вырезом на обложке. |

|
<= Рис. 7. |

|
Рис. 8. Копия обложки задачника с вырезом. =>
|
|
Тем же способом получена и следующая фотография (рис. 9). Зафиксируем мяч на полу. Чуть выше горизонтально поместим плакат, с предварительно сделанным отверстием (рис. 10), так, чтобы отверстие соответствовало контуру мяча. На фотографии создаётся впечатление, что мяч равен по диаметру отверстию в плакате, хотя на самом деле он намного больше по размеру (рис. 11). |
|
Рис. 9. |

|
Рис. 10. |


|
Рис. 11. |
|
Другая серия такого же рода оптических иллюзий может быть получена с помощью, так называемой искривленной комнаты Эймса, геометрия которой показана на рисунке 12. Сделана эта комната несколько необычно. Пол в ней наклонен и повышается вправо от наблюдателя, задняя стена удаляется по мере продвижения налево, окна на этой стене разных размеров, и имеют форму трапеции. Однако если в такую комнату смотреть из определенной точки, она выглядит совсем обычной: пол кажется ровным, задняя стенка - перпендикулярной направлению взгляда, а окна прямоугольными и одинаковыми. Эймс сделал одну из таких комнат достаточно большой для того, чтобы в ней могли находиться люди. Получился удивительный эффект: когда зритель рассматривает людей, прогуливающихся вдоль этой комнаты, он наблюдает необычайные изменения их размеров. В зависимости оттого, куда идет человек, он кажется то растущим, то уменьшающимся. Восприятие изображения – психологический процесс. При этом важно отношение наблюдателя к предмету наблюдения и даже его состояние в данный момент. Конечно, самим построить большую комнату Эймса довольно сложно. Но сделать небольшую модель можно. Помещая внутрь различные предметы, при желании можно получить довольно эффектные фотографии. |
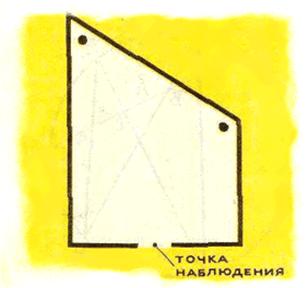
|
<= Рис. 12. Геометрия искривленной комнаты Эймса. |
|
Рис. 13. Развёртка искривлённой комнаты Эймса. => |
|
Возьмем два шарика для пинг-понга совершенно одинаковых по размеру. Для большей четкости изображения обернем их в черную эластичную ткань и поставим по углам модели комнаты. На фотографии (смотри рис.14) видно, что шарик, размещенный справа от наблюдателя, больше шарика, расположенного слева, в дальнем углу. При этом модель комнаты выглядит прямоугольной. Рассмотрим шахматные фигуры, помещенные в данную модель комнаты Эймса. Поместив по углам двух коней (из одного набора шахматных фигур), мы увидим, что правый конь больше левого (смотри рис.15), причем фигуры несколько наклонены влево, подтверждая наклон пола в данной модели комнаты Эймса. Поставим вдоль задней стенки модели ряд пешек (рис. 16). Заметим, как увеличивается их размер, по мере приближения от левого угла к правому, то есть от дальнего угла к ближнему углу. |

|
Рис. 14. |

|
Рис. 15. |
|
Рис. 16. |
|
Эти способы фотографирования до развития компьютерной графики имели широкое применение в студийной и художественной фотографии (например, виньетки). А так же использовались в кинематографии, особенно при съемках сказочных или фантастических фильмов. Благодаря этим иллюзиям любой человек, будь он кинорежиссёр или ученик, может создать собственные невозможные объекты. |
|
Список литературы: «Фотографирование невозможных объектов» В. И. Бахмин. |


